A partir de la fin du XVème siècle, on assista à la redécouverte de la géographie de Ptolémée et commencèrent les grands voyages d'exploration de Christophe Colomb, de Vasco de Gama, de Magellan. Pour la première fois, ces événements donnèrent à la cartographie sa dimension planétaire. De là, découle l'invention des premières projections cartographiques élaborées sur des bases mathématiques rigoureuses : la plus célèbre étant celle de Mercator en 1569.
1- La renaissance et le XVIIème siècle :
Si l'on excepte Henri le Navigateur, roi du Portugal (1394-1460), le souci principal des voyageurs n'était pas le perfectionnement des sciences. En effet, la lutte contre les Musulmans et les Vénitiens qui monopolisaient le commerce d'Orient poussèrent à chercher de nouvelles routes, à perfectionner les navires en "caravelles", à savoir déterminer la latitude au "bâton de Jacob" et à poser le problème de la longitude.
C'est Christophe Colomb qui découvrit la variation de la déclinaison de l'aiguille aimantée suivant les lieux (variation que nous représentons aujourd'hui pour une date nommée sur les cartes d'isogones).

Il crut que ces variations régionales étaient permanentes et qu'en les connaissant, on pourrait estimer la longitude du lieu où l'on se trouvait. Cet espoir fut vite déçu, et il fallut attendre les premières montres à ressort pour transporter l'heure et commencer à résoudre le problème de la longitude. Ce ne devait d'ailleurs être qu'au XVIIIème siècle que Cassini III allait déterminer avec précision, en Provence, une différence de longitude.

César-François Cassini dit Cassini III
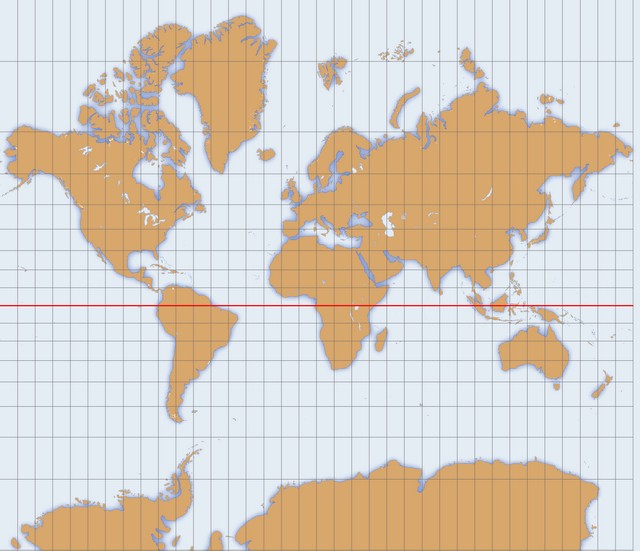
Cependant, même en l'absence d'une détermination précise des coordonnées géographiques, on essayait de reporter en place sur des canevas de projection les points connus. Pour exemple, la célèbre projection cylindrique dite de Mercator (Géographe flamand, de son vrai nom Gérard de Cremere, au service de Charles-Quint) fut publiée avec son atlas en 1569.

Gérard de Cremere - Mercator
La projection Mercator
La reproduction des cartes par gravure sur bois, puis sur cuivre, allait permettre d'éliminer les erreurs des copistes, et de les rependre en plus grand nombre. Très souvent, malheureusement, des soucis commerciaux ou politiques poussaient à falsifier les cartes afin de s'assurer le monopole de certains produits en gardant secrète la route qui y menait, et ainsi se perpétuaient des légendes.
Ce sont les besoins des Etats modernes (monarchie centralisées, empire napoléonien) désireux de connaitre leurs ressources générales, foncières et fiscales, de construire des canaux ou des routes stratégiques, qui ont fait franchir le pas décisif au moment même où le progrès scientifique le rendait possible.
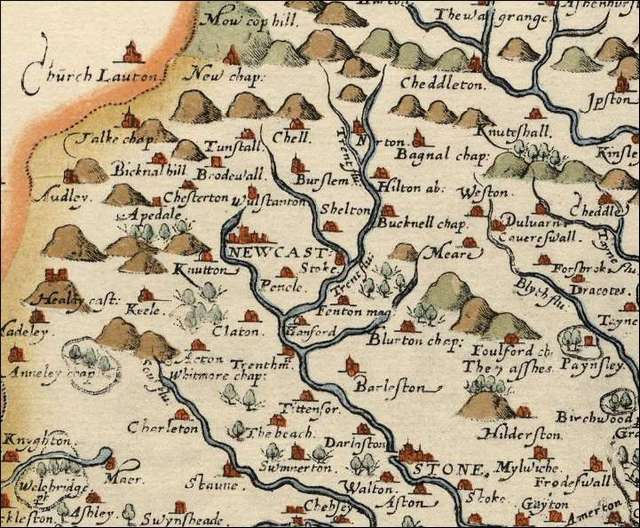
Fragment de la carte de Saxton de la Grande-Bretagne, partie du Kent - 1577
(Noter la figuration en perspective cavalière du relief, très schématisé et sans précision) et les villages (le clocher constitue une sorte de signe conventionnel)
Flu = fluivium (Latin) = rivière - Trent Flu. (Rivière Trent)
Mag. = Mangna (Latin) = grand - Fenton mag. (Grand Fenton)
Chap. = Chapelry (Village avec une église)
En revanche, si ce progrès devient surtout sensible au XVIIIème siècle, il ne faut surtout pas oublier l'apport précédent.

Galilée ou Galileo Galilei
C'est à la fin du XVIème siècle que, découvrant l'isochronisme des oscillations du pendule, Galilée (1564-1642) allait montrer l'importance de la constante "g" et permettre à Newton (1642-1727) d'envisager l'aplatissement terrestre aux pôles.

Isaac Newton
Cette théorie sera par la suite vérifié par les deux célèbres expéditions de Maupertuis, en Laponie (1898-1759), et de La Condamine (1701-1774), au Pérou en 1736.
Dès 1617, le Hollandais Snellius exposa les principes de la triangulation géodésique. Cependant, ce n'est seulement qu'en 1670 que l'abbé Jean Picard (1620-1682) effectua entre Paris et Amiens une première triangulation de grande précision. Il fut le premier à munir ses appareils de lunette de visée pour lesquelles il inventa le réticule, composé de deux fils croisés. Il fut également le premier à calculer le rayon de la Terre de façon précise, en mesurant un degré de latitude par triangulation le long du méridien de Paris. Ses mesures l'ont conduit à un résultat de 111 à 112 km pour un degré de latitude, ce qui donne un rayon terrestre de 6 372 km, le rayon polaire actuellement mesuré étant de 6 357 km.


2- Le XVIIIème siècle :
Au XVIIIème siècle, le développement de la cartographie est bien illustré par la réalisation de la carte de Cassini III au 1/86.400e, commencée en 1747 et achevée sous la Révolution. C'était pour l'établir que Cassini II avait entrepris en 1733 la mesure d'un arc de parallèle de Strasbourg à Brest.
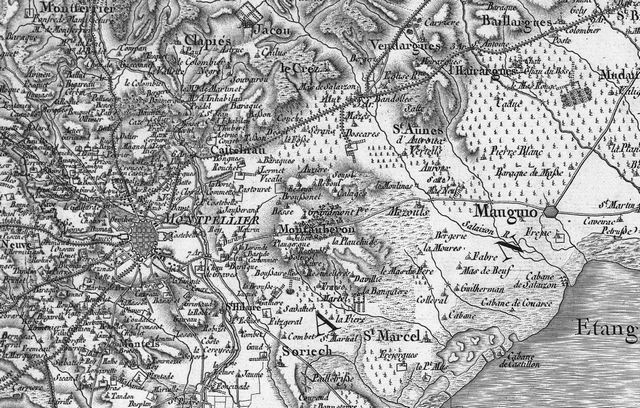
Extrait de la carte de Cassini (Partie Sud de l'Hérault)
La Carte de Cassini, appelée aussi Carte de l'Académie, est la plus ancienne carte détaillée de la France. Elle fut dressée par la famille Cassini, principalement César-François Cassini (Cassini III) et son fils Jean-Dominique Cassini (Cassini IV) au XVIIIe siècle, à l'échelle d' une ligne pour cent toises, autrement dit une échelle de 1:86400e. 1 centimètre sur la carte correspond à environ 864 mètres sur le terrain. Les levées ont été effectuées entre 1756 et 1787 et les 181 feuilles composant la carte ont été publiées entre 1756 et 1815.
Cette carte constituait pour l'époque une véritable innovation et une avancée technique décisive. Elle est la première carte à s'appuyer sur une triangulation géodésique dont l'établissement prit plus de cinquante ans. Les quatre générations de Cassini se succédèrent pour achever ce travail.
Ces techniques permettaient en effet des mesures de plus en plus précises. C'est à d'Alembert (1717-1743), Clairaut (1713-1765) et Euler (1707-1783) que l'on doit des progrès décisifs dans l'amélioration des objectifs composés permettant un raccourcissement des lunettes. La mesure des angles, à l'aide d'un cercle gradué, devenait plus sûre depuis que ceux-ci pouvaient être réalisés avec les premières machines à diviser les cercles du duc de Chaulhes (1717-1783).
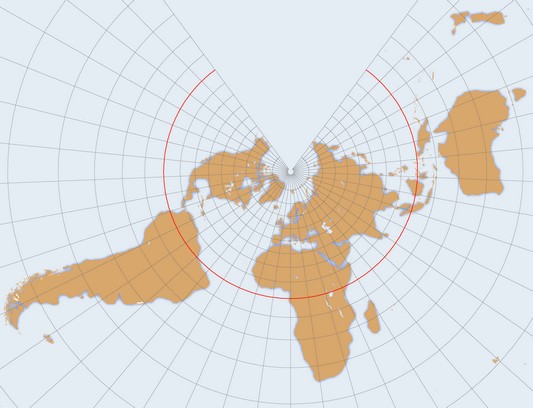
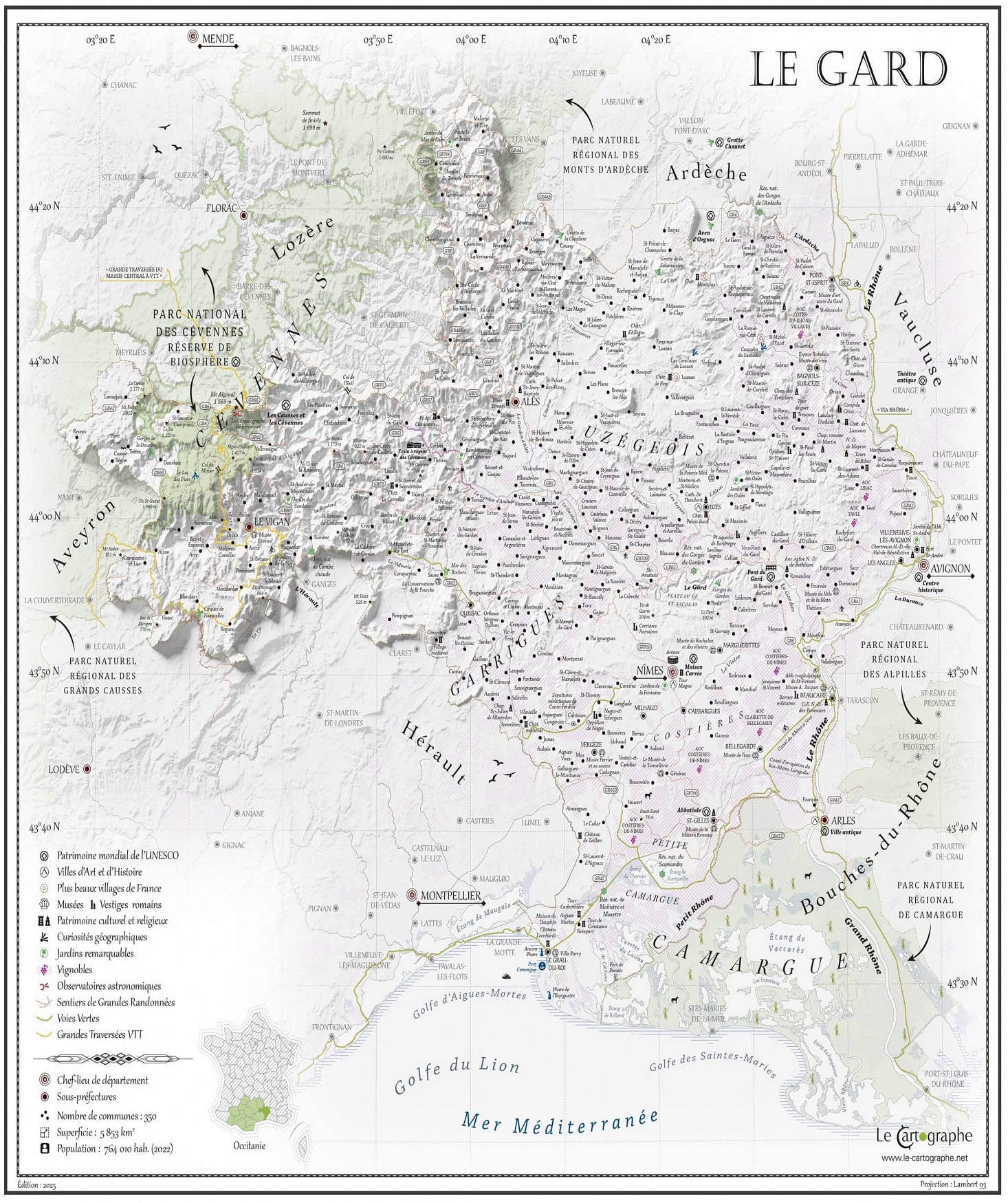
Newton indiquait le principe du sextant. Les mesures de longueur directes à la latte purent approcher une grande précision grâce aux règles bimétalliques de Borda (1733-1799). En même temps, de nouvelles projections étaient proposées, clarifiant les notions de conformité et d'équivalence ; par exemple la projection conique de Lambert (1728-1777), adoptée pour la nouvelle carte de France au 1/50 000e, commencée en 1920.
La projection conique de Lambert
Cependant ce ne fut qu'au XIXème siècle que Gauss résolut le problème de la représentation conforme de l'ellipsoïde sur le plan de la carte : la terre correspond à un ellipsoïde de révolution applati aux pôles et non à une sphère.
Sources :
- Travaux pratiques de géographie de J. Tricart, M. Rochefort et S. Rimbert aux éditions SEDES
- Wikipédia, l'encyclopédie libre